本文共 4060 字,大约阅读时间需要 13 分钟。
缘起
Android上硬件编解码一直是个老大难问题,就解码来说,硬解码本身并不困难,只要按照MediaCodec的流程开发即可。但由于系统碎片化,硬件规格不一致,硬件解码会到黑屏,花屏,绿屏之类的显示问题。为了不招致用户投诉,我们在做视频解码的时候不太敢开启硬件加速,一般会采用保守策略,即以软解为主,优先保证画面正常,但牺牲了性能。
一般解决这个问题的方案是使用黑(白)机型名单下发配置(如:腾讯视频),或者暴露开关让用户手动去控制是否走硬件解码(如:bilibili)。
使用机型黑(白)名单有一定的作用,但其问题也显而易见:
- 需要浪费大量的人力,精力进行机型测试,去维护,发布名单
- 覆盖度偏低,一般只覆盖TOP机型
- 缺乏时效性,例如新机型上市不能及时跟进
- 不一定准确,因为硬解是否成功,跟视频源也有很大关系,同一个机型可能解这个视频不成功,另外一个视频又是成功的。按照机型\u0026quot;一刀切\u0026quot;的前提是要保证视频规格一致,这样才最健壮。
通过开关让用户切换体验太差,尤其是“抖音”之类的短视频App,总不能每个界面加个开关让用户去切换解码器这么深奥的东西吧,从用户角度讲,我为什么要关心这个什么解码器怎么设置,只要视频能正常看就行。
仔细思考一下,我们其实可以实现自动化的检测,即模拟人工检测流程,把样本视频各软硬解一遍,然后对比他们的解码结果(图片)就能够知道硬解码是否能跑通。解码的流程轻车熟路,那么这里的关键问题就是我们如何进行图片对比?如何量化图片的差异度?
图片检索技术
图片对比其实跟\u0026quot;以图搜图\u0026quot;本质上是同一种技术,通常有几种做法MSE,均值哈希,色彩直方图以及OpenCV里面一些提取图像特征的高级算法,如Sift,Surf等。基于移动端的运行效率,安装包大小,以及需求本身考虑,我们放弃引入OpenCV。MSE 属于逐像素对比,对像素值要求过于严格,太简单粗暴,色彩直方图不太好量化差异度。基于以上考虑,我们选择图像哈希算法,它可以输出汉明距离,方便量化软硬解结果的差异度。
哈希算法有三种,平均哈希,感知哈希和差异度哈希,基于准确度考虑,我们选择实现较复杂一些的感知哈希算法。另基于性能考虑,我们在Android平台上使用C++实现算法,通过JNI接口给Java调用。Java层输入Android的Bitmap对象,输出为图片指纹,再通过对比指纹的汉明距离,我们即可判断出来解码是否正常。
Java层接口签名如下:
public native long getHash(Bitmap bitmap, int algorithm);public native long getHammingDistance(long hash1, long hash2);
下面分析一下感知哈希实现的方法和背后的原理,使之知其然,知其所以然。
图片的构成

 图二
图二 我们知道图片由RGB三原色构成这称之为加色法,我们可以认为图片有三个维度(暂不考虑Alpha)。分析上面两幅图,图一为原图,可以发现图片里蕴含的大部分信息都是低频的,比如天空,绿叶,树枝等,他们很少变化。高频信息是小鸟的眼睛,嘴巴等细节。图二是把图一经过缩放且只保留亮度信息,可以看到这有效的移除了图片的细节,即高频信息,展示了图片的低频部分。图片的低频部分决定了图片的大体结构,高频部分则完善了图片的细节。我们在对比图片是否相似的时候,其实更关注的是中低频部分的差异度。
在实践中,我们可以把图片从RGB转换为YCbCr格式,只提取Y的部分参与计算,实现降维,以减少运算量。再把图片缩放到32*32大小,丢弃掉大部分高频信息。由于进行了降维和缩放,后续步骤我们的运算量已大大减少。
把图片从空域转换到频域,我们需要使用DCT(二维离散余弦变换)。DCT也是JPEG以及H264压缩算法的核心部分,感兴趣的可以继续深入了解视频压缩算法的相关研究。感知哈希与DCT(离散余弦变换)
为了让大家深入了解背后的原理,这里打算展开介绍一下DCT,以及它为什么能检测出来图片的相似程度。本文恐怕是网络上能找到讲解DCT最详细的一篇文章了,如果你对背后的原理不感兴趣,也可以直接跳过。
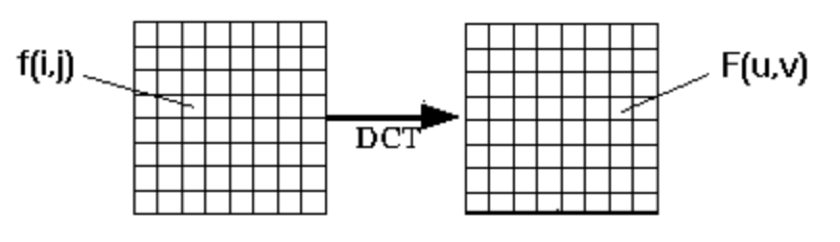
DCT由如下的公式定义,N和M为矩阵的行数和列数
$$
\\begin{equation}F(u, v) = \\left (\\frac{2}{N} \\right )^{\\frac{1}{2}} \\left (\\frac{2}{M} \\right )^{\\frac{1}{2}} C(u)C(v) \\sum_{i=0}^{N-1}\\sum_{j=0}^{M-1} f(i,j)cos\\left [\\frac{\\left(2i+1\\right)u\\pi}{2N} \\right ]cos\\left [\\frac{\\left(2j+1\\right)v\\pi}{2N} \\right ]\\end{equation}$$$$
C(\\varepsilon) =\\begin{cases}\\frac{1}{\\sqrt{2}}\u0026amp; \\text{for}\\ \\varepsilon = 0\\\\\\1\u0026amp; \\varepsilon\u0026gt;0\\end{cases}\\$$其中:
- u,v = 离散频率变量(0,1,2…7)
- f(i,j) = 图像在i行j列的像素值
- F(u,v) = DCT结果
我们先研究一个最简单的场景,假设图片像素值如下:
$$
\\begin{bmatrix}1 \u0026amp;3 \\\\\\2\u0026amp; 0\\end{bmatrix}$$当N和M都为2时,上述公式可简化为:
$$
\\begin{equation}F(u,v) = C(u)C(v) \\sum_{i=0}^{1}\\sum_{j=0}^{1} f(i,j)cos\\left [\\frac{\\left(2i+1\\right)u\\pi}{4} \\right] cos\\left [\\frac{\\left(2j+1\\right)v\\pi}{4} \\right]\\end{equation}$$下面我们来计算二维DCT
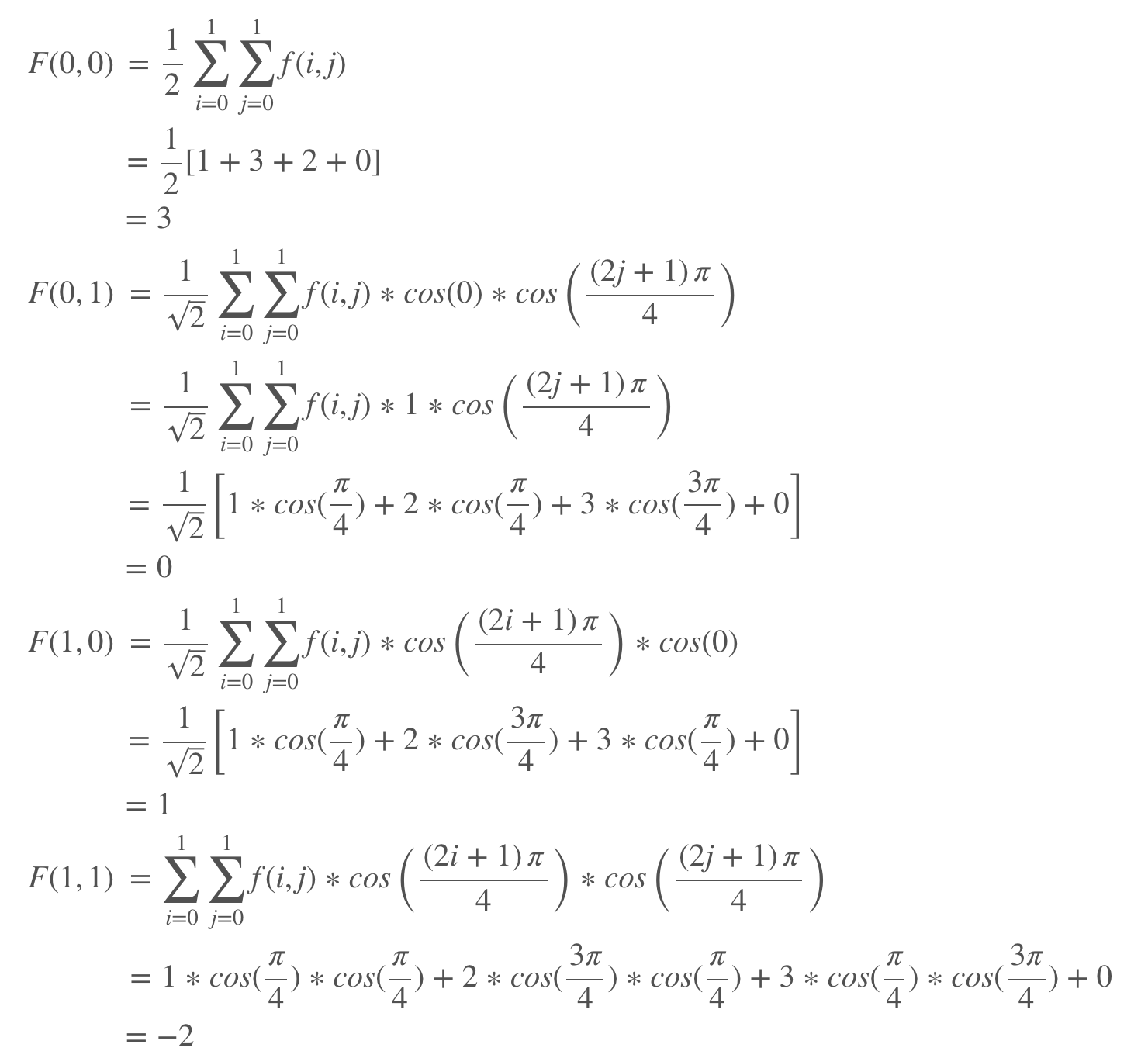
即,结果是:
$$
\\begin{bmatrix}3\u0026amp;0\\\\\\1\u0026amp;-2\\end{bmatrix}$$用Python的相关模块可以交叉验证我们的计算结果:
\u0026gt;\u0026gt;\u0026gt; import numpy as np\u0026gt;\u0026gt;\u0026gt; from scipy.fftpack import dct\u0026gt;\u0026gt;\u0026gt; d=np.matrix([[1,3],[2,0]])\u0026gt;\u0026gt;\u0026gt; dct(dct(d,axis=0,norm=\u0026quot;ortho\u0026quot;),axis=1,norm=\u0026quot;ortho\u0026quot;)array([[ 3., 0.], [ 1., -2.]])
在实践上,上述方式的计算效率不高,更加简便的计算方式是使用DCT矩阵:
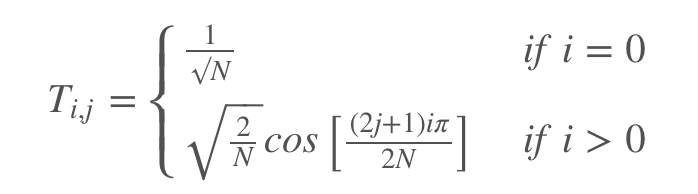
若N取2,得到DCT矩阵
$$
\\begin{vmatrix}\\frac{1}{\\sqrt{2}} \u0026amp; \\frac{1}{\\sqrt{2}} \\\\\\cos(\\frac{\\pi}{4}) \u0026amp; cos(\\frac{3\\pi}{4})\\end{vmatrix}$$若N取8,得到的矩阵是这样的

其中i=0时,即第0行,称为DC分量,i=1-7成为AC分量,用图表形式表示如下
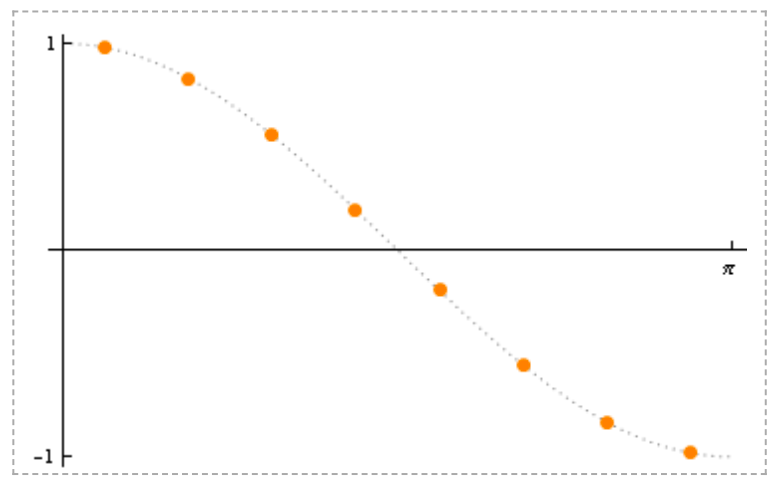
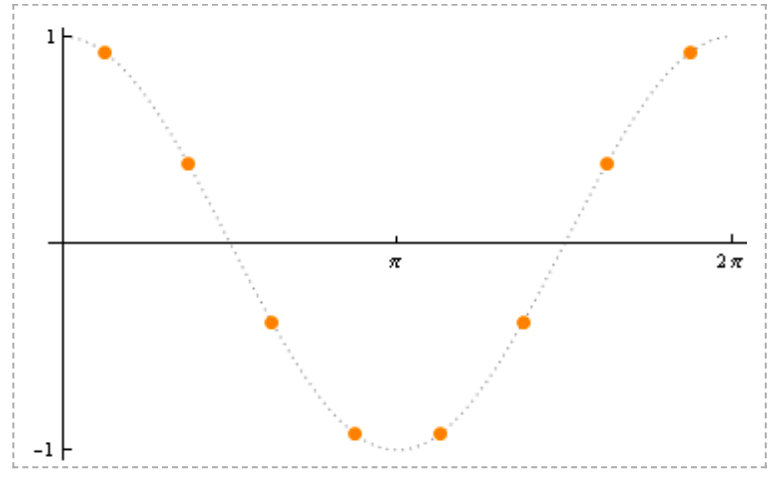 i=2
i=2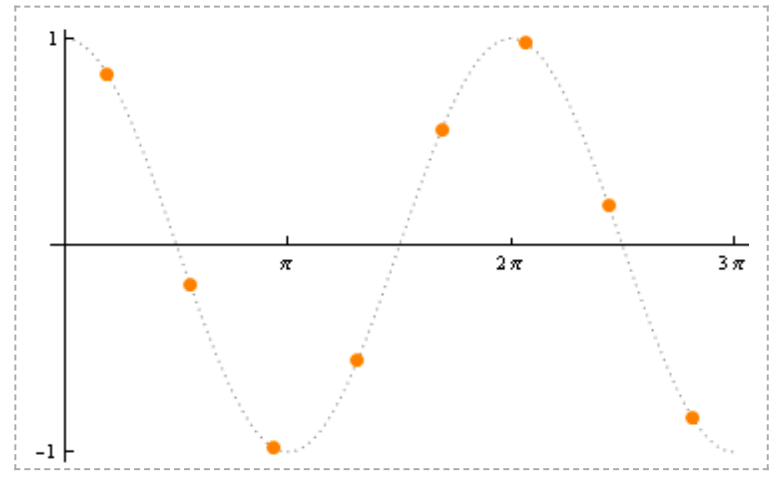 i=3
i=3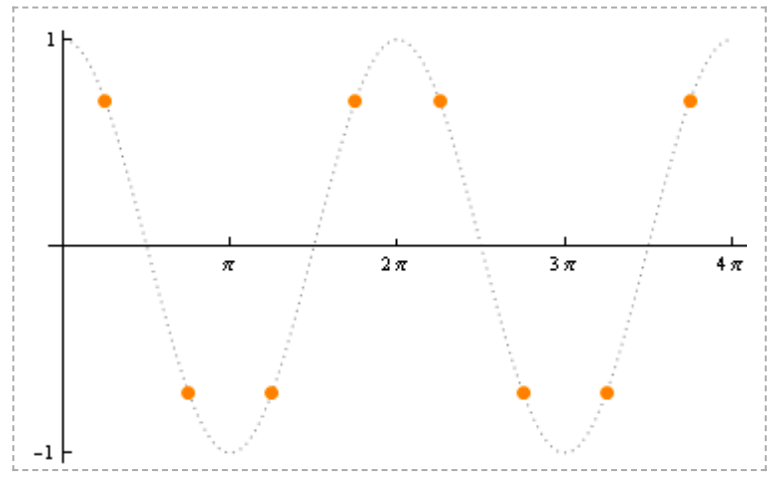 i=4
i=4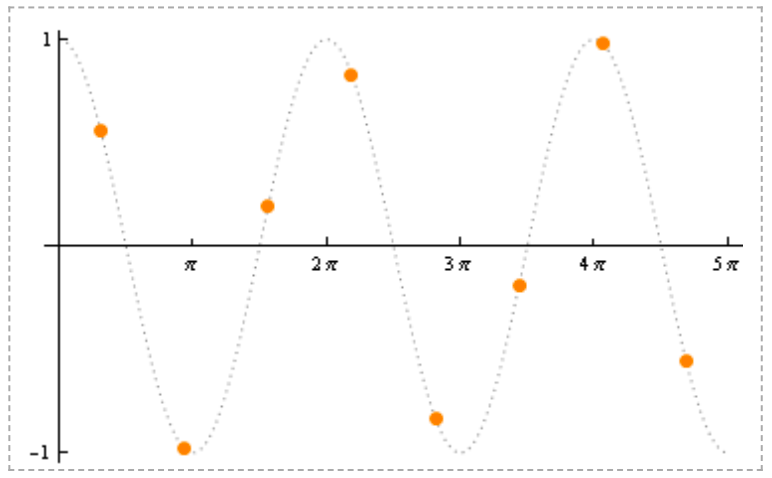 i=5
i=5 i=6
i=6 i=7
i=7 有这样一个矩阵的话,我们再进行DCT变换就非常简单了:
$$
D=TMT^T$$其中:
- T = DCT矩阵
- M = 图像数据
- D = DCT结果
这是对一张8*8图片应用DCT变换得到的矩阵结果:
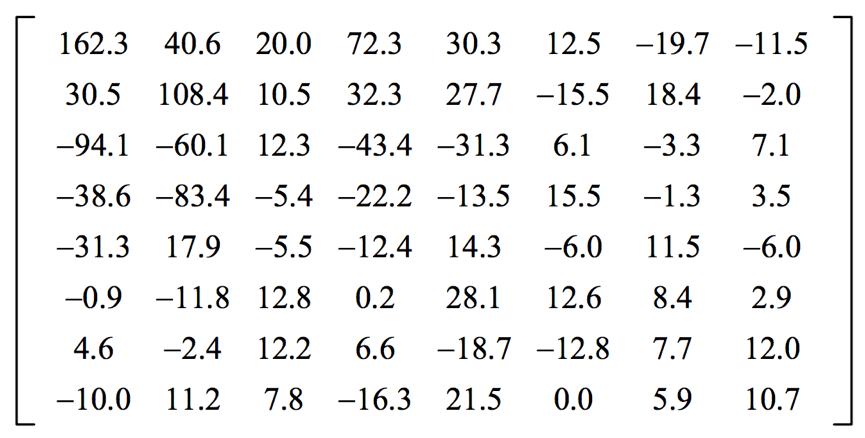
这个矩阵最左上角是低频信息,右下角是高频信息。有个神奇的东西叫基准样式。

信不信由你,任意一张8*8的图,都可以由标准图中的的小图以一定比例叠加而合成,而每个小图的权重,由DCT变换得到的矩阵决定,是不是很有意思。DCT变换后左上角一般是比较大的数字,而右下角一般是比较小的数字,这暗含了图片中低频信息占的比重较多,因此我们在做图片或者视频编码压缩的时候,正是通过量化舍弃右下角的高频信息,来实现信息的压缩。
图片差异度
我们在对比图片差异的时候,正是通过对比频域信息来实现的。在我们的实现中,首先把软硬件解码后的图片转成YCbCr格式,只提取其中的Y,实现降维,再把图片缩放到32*32大小,进一步减少运算量,同时舍弃了一部分高频信息。再应用32*32的DCT把图片转换到频域,从频域矩阵中提取8*8中低频区域的系数,计算算数平均值。
$$
D = \\frac{\\sum_{i=2}^{9}\\sum_{j=2}^{9}f(i,j)}{64}$$矩阵中的每个值再与D比较,大于D计1,小于D计0,按位存储,我们即可得到一个图片指纹。通过计算两个图片指纹的差异,我们就可以得到可以量化图片差异度的数字。
当差异为0时,我们认为两张图片完全一样,差异越大,表明图片越不相似。对于解码出现绿屏,花屏的情况,我们可以有效的检测出来。绿屏案例,相似度24:

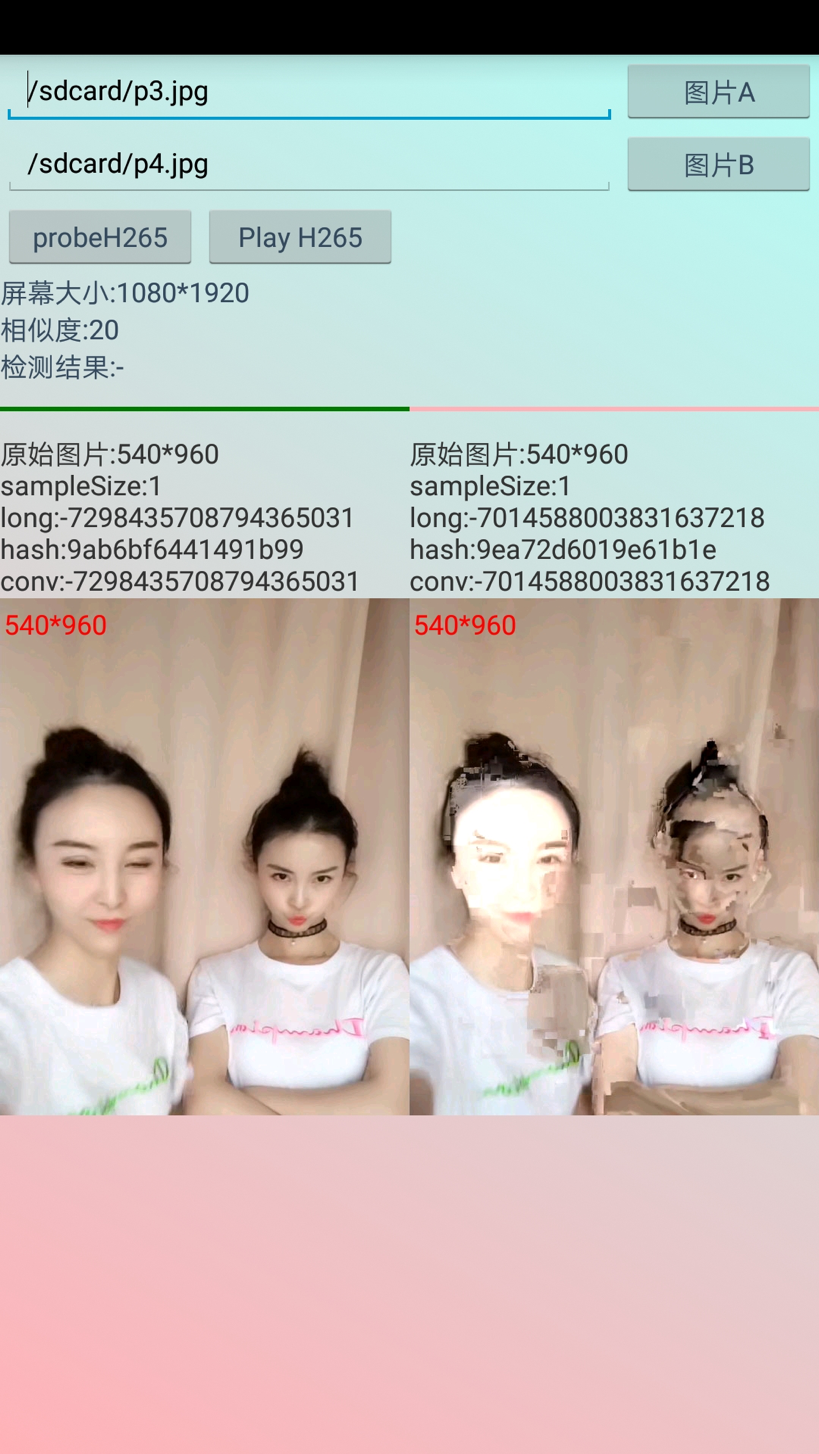
花屏案例,相似度20:

检测Demo截图:
转载地址:http://tvyqa.baihongyu.com/